1232. SKYLINE
The skyline of
Singapore as viewed from the Marina Promenade is one of the iconic scenes of
Singapore. Country X would also like to create an iconic skyline, and it has
put up a call for proposals. Each submitted proposal is a description of a
proposed skyline and one of the metrics that country X will use to evaluate a
proposed skyline is the amount of overlap in the proposed sky-line.
As the assistant to
the chair of the skyline evaluation committee, you have been tasked with
determining the amount of overlap in each proposal. Each proposal is a sequence
of buildings (b1, b2, …, bn),
where a building is specified by its left and right endpoint and its height.
The buildings are specified in back to front order, in other words a building
which appears later in the sequence appears in front of a building which
appears earlier in the sequence.
The skyline formed by
the first k buildings is the union of the rectangles of the first k buildings
(see Figure). The overlap of a building, bi, is defined as
the total horizontal length of the parts of bi, whose height
is greater than or equal to the skyline behind it. This is equivalent to the
total horizontal length of parts of the skyline behind bi which
has a height that is less than or equal to hi, where hi
is the height of building bi. You may assume that
initially the skyline has height zero everywhere.
Input. The input consists of a line containing the number c
of datasets, followed by c datasets, followed by a line containing
the number `0'.
The first line of each
dataset consists of a single positive integer, n (0 < n < 100000),
which is the number of buildings in the proposal. The following n lines
of each dataset each contains a description of a single building. The i-th
line is a description of building bi. Each building bi
is described by three positive integers, separated by spaces, namely, li,
ri and hi, where li and rj
(0 < li < rj ≤ 100000) represents the left and right end point of the
building and hi (0 < hi ≤ 109)
represents the height of the building.
Output. The output consists of one line for each dataset. The
c-th line contains one single integer, representing the amount of overlap
in the proposal for dataset c. You may assume that the amount of overlap
for each dataset is at most 2000000.
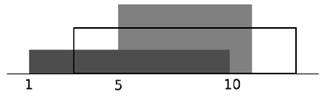
Note: In the sample test case, the overlap of building b1,
b2 and b3 are 6, 4 and 4 respectively. Figure shows how to
compute the overlap of building b3. The grey area represents the skyline
formed by b1 and b2 and the black rectangle represents b3.
As shown in the figure, the length of the skyline covered by b3 is from
position 3 to position 5 and from position 11 to position 13, therefore the
overlap of b3 is 4.
Sample Input
1
3
5 11 3
1 10 1
3 13 2
0
Sample Output
14
РЕШЕНИЕ
дерево отрезков
Анализ алгоритма
Заведем дерево, поддерживающее минимум и максимум на
отрезках. Листья дерева отрезков соответствуют
интервалам длины 1. То есть зданию от позиции a до позиции b
соответствует отрезок [a; b – 1]. Например, если здание соединяет
соседние позиции a и a + 1, то ему соответствует отрезок
единичного размера [a; a].

Если на отрезке [a;
b] линия горизонта имеет одну высоту,
то минимум и макимум в соответствующих ему фундаментальных отрезках одинакова. Рассмотрим следующий тест:
3
3 6 4
2 7 3
1 4 1
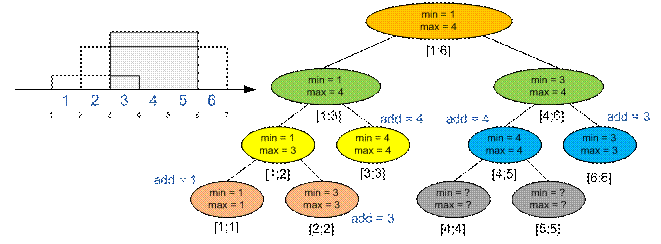
В переменной add указаны высоты отложенных операций.
Здания обрабатываем,
последовательно добавляя их в дерево отрезков и вычисляя их линию горизонта. При добавлении дома [a; b]
высоты h разбиваем отрезок на
фундаментальные [ai; bi] и на каждом из них:
·
если высота h меньше минимума на [ai; bi], то ничего не делаем (возвращаемся) поскольку линия
горизонта не меняется;
·
если высота h больше или равна максимуму на [ai; bi], то присваиваем отрезку [ai; bi] значение минимума и максимума равным h, создаем отложенную операцию
присваивания add = h и включаем отрезок длины bi – ai + 1 в линию горизонта для текущего рассматриваемого
здания. Отметим, что если высота h равна максимуму на [ai; bi], то отрезок [ai;
bi] текущего здания
принадлежит линии горизонта;
·
если даже отрезок
запроса [x, y] совпадает с фундаментальным [a;
b] (x = a, y = b),
но при этом на нем минимум не равен максимуму и min ≤ h < max, то продолжаем делить
фундаментальный отрезок (он не является листом) и совершаем запросы на
сыновьях.
Реализация алгоритма
#include <cstdio>
#include <algorithm>
#include <cstring>
#define MAX 100010
using namespace
std;
struct node
{
int min, max, add;
} SegTree[4*MAX];
int tests, i, n, x, y, h, res;
void Push(int
Vertex, int LeftPos, int
Middle, int RightPos)
{
if (SegTree[Vertex].add != 0)
{
SegTree[2*Vertex].add = SegTree[2*Vertex+1].add = SegTree[Vertex].add;
SegTree[2*Vertex].min = SegTree[2*Vertex+1].min = SegTree[Vertex].add;
SegTree[2*Vertex].max = SegTree[2*Vertex+1].max = SegTree[Vertex].add;
SegTree[Vertex].add
= 0;
}
}
void Modify(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right, int Height)
{
if (Left > Right) return;
if (SegTree[Vertex].min > Height) return;
if ((LeftPos == Left) && (RightPos == Right))
{
if (Height >= SegTree[Vertex].max)
{
res += Right -
Left + 1;
SegTree[Vertex].add = SegTree[Vertex].min =
SegTree[Vertex].max = Height;
return;
}
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
Modify(2*Vertex,
LeftPos, Middle, Left, min(Middle,Right), Height);
Modify(2*Vertex+1,
Middle+1, RightPos, max(Left,Middle+1), Right, Height);
SegTree[Vertex].min =
min(SegTree[2*Vertex].min,SegTree[2*Vertex+1].min);
SegTree[Vertex].max =
max(SegTree[2*Vertex].max,SegTree[2*Vertex+1].max);
}
int main(void)
{
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
memset(SegTree,0,sizeof(SegTree));
res = 0;
for(i = 0; i < n; i++)
{
scanf("%d %d %d",&x,&y,&h); y--;
Modify(1,1,MAX-1,x,y,h);
}
printf("%d\n",res);
}
return 0;
}